A publican received a 3.5% exchequer on the sale of a house that costs $200,000. What is the amount, in dollars, of the exchequer? [exchequer = sale price x stripe]
Wednesday, March 27, 2013
I Don't Get This Either
It's always helpful, I think, to step back from the question of education and just think about learning. Suppose you're curious about something. Like maybe articles about the recent banking crisis in Cyprus have made you curious about the island's history. The best first step, by far, is to go to the "History of Cyprus" Wikipedia page and read it. If you're still interested, maybe follow up with a book or two. Watching a person stand up and talk about Cyprus is pretty far down the list, whether you're watching the person live or on a video. It's true that if you want to learn how to tie a bowtie or to properly flip a Spanish tortilla, you may want to watch a video. The visual information is very helpful when you're talking about demonstrating a physical action. But to convey information? Reading is faster than listening, and buying a book—or checking one out from a library—has always been cheaper than paying college tuition, in part because when you go to college you still have to buy all these books.
Especially people who are excited about the Common Core should not be excited about the promise of students watching videos -- the entire premise of the CC is that reading complex texts independently is the most important thing!
Takeaway from Yesterday's Mucking About
It is clear that the discontinuity (i.e., significant drop) in NECAP math scores between 8th grade and 11th was entirely anticipated and intentional. Whether or not that's a good idea, or why it was done, I can't say. But anyone who looks at the relative proficiency rates and concludes that they indicate a drop in performance or achievement in high school doesn't understand the situation. Primarily the test is harder. The NECAP doesn't tell us anything conclusive about whether teaching and learning is better or worse between our middle school and high school math instruction.
Tuesday, March 26, 2013
Random Nugget from the NECAP Weeds
2007-2008 NECAP Math Reading Writing Technical Report with Appendices, Appendix F, Page 54:
3. A psychometrician will present and explain the average bookmark placement for the wholegroup based on the Round 2 ratings. Again, based on their Round 2 ratings, panelists will know where they fall relative to the group average. The psychometrician may also present impact data, showing the approximate percentage of students across the three states that would be classified into each achievement level category based on the room average bookmark placements from Round 2.
So basically the panel went through the process of setting, discussing and revising 11th grade math cut scores twice, and only then someone may have pointed out that according to what they had done so far, probably about 40-50% of the students in their state would receive the lowest score and less than two percent would get the highest (of 4), before going through one more revision.
The panel thought the impact data (if they got it) was the least important factor in their decision (average rating of 2.7).

The most important factors to them were their own experience and the items themselves, which makes sense, except that the range of item difficulty was very high compared to other NECAP and NAEP tests, so that would skew the whole standards-setting process from the start.
That's all fine for just comparing schools, districts, or even students, but it is not at all how you'd look at setting the cut scores for a graduation test. A single graduation test that would put 45% of all juniors at direct risk of failure and retention would demand more serious consideration of "impact analysis."
Learning Progressions Frameworks Designed for Use with The Common Core State Standards in English Language Arts & Literacy K-12
I came across this while mucking about the National Center for the Improvement of Educational Assessment website. The Learning Progressions Frameworks Designed for Use with The Common Core State Standards in English Language Arts & Literacy K-12 is sort of a compatibility layer (to use an IT term) between Common Core and how actual English teachers look at the discipline. You know, using words like "genre" and "persuasive techniques," or "habits and dispositions of reading."
To me, it is a more sane expansion of the standards to better reflect the full discipline of English Language Arts.
Another Head Scratcher
RIDE's sorta-response to NECAP criticism (posted by Elisabeth Harrison here) concludes with some examples of test items and the % of students "not meeting the graduation requirement" (so, scoring a "1," presumably) who got the question right. Here's the first example:
A real-estate agent received a 3.5% commission on the sale of a house that costs $200,000. What is the amount, in dollars, of the commission? [commission = sale price x rate]
Only 6% of students scoring a "1" overall got this correct. Which is weird because it is trying hard to tell you that it is just a multiplication problem. This seems to be the easiest of the four questions listed, but it has the lowest correct rate by far. And in general "numbers and operations" is the lowest scoring component in the 11th grade NECAP, and much lower scoring (by about 20%) than the equivalent 8th grade component.
So... I don't know. It just seems strange. Is more numbers and operations drill the best strategy for improving your NECAP math score for graduation even though it is a relatively small section?
If 11th Grade NECAP Math was Aligned with Other Assessments, It Would Be... A Lot Easier
This is from the Explain To Me Why My Interpretation Is Incorrect file.
So Tom Sgouros finally dragged me into the weeds of the NECAP technical documentation, and I found an interesting passage regarding the process of setting the cut-points for NECAP 11th grade math Achievement Level Descriptions. This is from the Collection and Analysis of Existing Performance Data section on page 311 of the 2007-08 NECAP Technical Report. the "ordered item booklet" has test items in order from easiest to most difficult.
Existing Test Data. Two categories of existing test data were examined: 1) fall 2007 scores in grades 6 through 8 and 2) historical performance on other high school-level tests (for example, NAEP).
For reading, starting cut-points were calculated from the existing test data as follows: the pattern of performance on the fall 2007 NECAP reading tests in grades 6, 7, and 8, was determined (specifically, the percentage of students in each achievement level category). Predicted grade 11 scores were then calculated by extrapolation. The resulting cuts were found to be in line with other high school-level testing data and to represent reasonable starting points. Therefore, they were adopted as starting cuts for standard setting. The starting cuts were presented to panelists as placements in the ordered item booklet (see below for complete details), and panelists were asked to either validate the placements or recommend modifications.
For mathematics, potential starting cuts were calculated in the same way as for reading, but were not used for standard setting. The purposes of using starting cuts are to streamline and simplify the standard-setting process and to make use of any other relevant sources of available information. However, the grade 11 mathematics test was quite difficult for the students, and the extrapolated starting placements for the lower two cuts appeared very early in the ordered item booklet (specifically, between ordered items 1 and 2 and between ordered items 6 and 7). This anomaly suggested that differences between the grade 11 mathematics test and the previously existing data rendered the use of those data, and the resulting cuts, inappropriate. In addition, it was feared that the use of such low starting cuts would complicate the process for the panelists and possibly impact the validity of the results negatively. For these reasons, a standard-setting, rather than a standards- validation, approach was adopted for mathematics.
Let me emphasize that:
the extrapolated starting placements for the lower two cuts appeared very early in the ordered item booklet (specifically, between ordered items 1 and 2 and between ordered items 6 and 7)
So based on extrapolation of performance on other comparable tests, the cut-point between scoring a "1" and "2" on the 11th grade NECAP math (aka, not-graduating or graduating) would have come after answering two questions correctly. And scoring "3" -- proficient -- would have required seven correct answers out of 40 or more questions.
Later... OK, here's why I struck that paragraph and changed the title (quoting the instructions for the cut-point setting process):
- What you need to know is that the ordered item cut point for a given cut does not equal the raw score a student must obtain to be categorized into the higher achievement level
- For example, if the Substantially Below Proficient/Partially Proficient cut is set between ordered items 3 and 3, this does not mean that a student only need sot get 4 points on the test in order to be classified into the Partially Proficient level
There is a reason I don't plunge this deep into the weeds if I can avoid it.
Nonetheless, the fact remains that the cut-points extrapolated from NAEP and other NECAP scores were so low compared to the difficulty of the items in the ordered item booklet that NECAP chose to not show them at all.
Pointing that out to panelists certainly would have "complicated the process" of setting much higher cut points. Not just high in comparison to other slacker, racing-to-the-bottom states. Higher in comparison to other NECAP math tests and NAEP.
Nobody Wants to Just Say the 11th Grade NECAP Math is Too Hard, But That's the Problem
So RIDE sorta responded to Tom Sgouros's critique of the use of the NECAP for a graduation requirement. My sense of the technical points is that Tom is right about how the items are chosen, but underplayed the decisive role of the overall difficulty and cut scores in NECAP 11th grade math.
The bottom line is this: if at the end of your testing process you end up with something that looks like this:
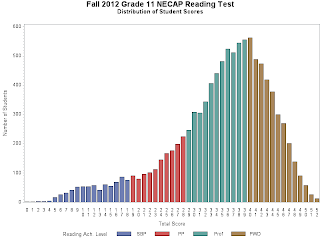
Nobody is going to complain too much.
If you start closing schools and threatening to retain students based on this:
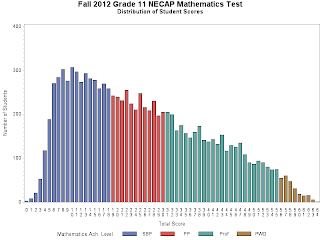
You're going to have problems.
Monday, March 25, 2013
Can't Really Argue With These Points
4) Common Core is providing license to all sorts of crazy and contradictory local policies. Districts are cutting literature, pushing back Algebra, increasing constructivist approaches, reducing constructivist approaches… all in the name of Common Core. When parents and local voters complain, the schools dodge accountability by claiming (perhaps falsely) that Common Core made them do it. A big danger of trying to build a centralized system of controlling schools is that local education leaders will blame the central authority for whatever unpopular thing they choose to do. It’s like the local Commissar blaming shortages on the central authority rather than his own pilfering. It shifts the blame.
5) Common Core is bringing out the worst in many of its advocates — people who are not naturally inclined to be hypocrites, sycophants, and dissemblers, but who cannot resist becoming so because of the lure of power, money, and the need to remain relevant. If you need examples of this, well, you probably haven’t been reading this blog.
Well, I'm not so sure they aren't so "naturally inclinded."
Trying to Find the 11th Grade NECAP Storyline
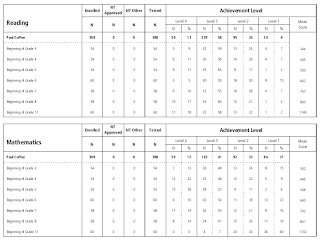
Take a look at the Paul Cuffee (charter) School NECAP scores for this year:
Cuffee has somewhat easier demographics than PPSD, but is pretty representative of the city as a whole. As you can see, they have good results across the board, very consistent, except 11th grade math. This is the high school's third year and their first 11th grade NECAP scores. While they've got 80% proficiency in 5th grade math and 76% proficiency in 11th grade reading, it is down to 7% for 11th grade math. 60% of Cuffee juniors are at risk of not graduating because of math.
- It isn't because of the union or lazy teachers with tenure.
- It isn't because they haven't had time to understand or adjust to the NECAP -- the test was well established when the school was started and the curriculum was designed.
- I believe most if not all their students were recruited from their middle school, so that should be a solid base of achievement coming in.
- They didn't have to recruit a whole host of math teachers; presumably just one per grade, for a well-regarded charter. If they can't find two or three good math teachers -- if that's actually the problem -- then... well, our "theory of change" is just broken.
- You can't claim that the school just doesn't understand "data-driven instruction" or "accountability" or whatever, because all their other scores are fine.
Here's something else I noticed that has me scratching my head. The mean scaled score for Cuffee in 11th grade math is 1132, statewide it is 1135, but the difference in proficiency rates are 7% for Cuffee and 32% for the state. That seems like a pretty huge change in proficiency rate for a 3 point swing in scale score.
Friday, March 22, 2013
Pieces of inBloom
Looking at the inBloom Data Ingestion Specification, here are some of the key open source (or not) components of the system:
- Database: MongoDB
- Identity Provider: SimpleIDP (proprietary)
- Directory Service: OpenLDAP
- Distributed Filesystem: GusterFS
- Message Queue: ActiveMQ
- Search: ElasticSearch & Lucene.
- FTP: ProFTPD
- Random bits: Maestro nodes? Pit nodes?
In other news, the Death Star runs Linux!
Thanks to the Providence Student Union and Aaron Regunberg
Just wanted to put out an extra word of appreciation to the kids in the Providence Student Union and especially Executive Director Aaron Regunberg for orchestrating and executing the Take the Test! action. They really seized the initiative and controlled the news cycle here for a solid week, knocking Commissioner Gist off her game and out of her comfort zone for more or less the first time in her tenure here. Excellent work.
Maybe even more importantly, the national attention brought to this action can be a model for more pre-emptive actions around the Common Core assessments, including simply making people aware of the importance of being able to access sufficient examples of the difficulty of a high-stakes exam.
Reminds Me of Another Math Test I Took Recently
To his benefit, the student although learning disabled has strong intellectual potential that enables him to easily learn the various strategies I and his teachers have developed to help him do the math. Yet, when tested on these concepts, he mostly gets grades in the low seventies on tests in which problems contain three or more steps and which requires him to describe using mathematical terms various math processes. One problem he got wrong had to do with the Pythagorean Theorem. Mathematically, he knows the formula and can apply it to solve problems presented algebraically. He understands that if we want to find the unknown length of one side of a right triangle, he can do so as long as he knows the length of a hypotenuse and an adjacent side. However, on a test in which a problem derived from a sample CCLS standard, he got completely lost. The problem had a right triangle containing adjacent squares for each side. The question asked what assumption the student can make about the area of the largest square. Furthermore, he was expected to explain his assumption in mathematical terms.
After looking at the problem, it appeared familiar to me. I then remembered where I saw a similar problem. I decided to take a trip to my attic and opened up an old box. Within the box, I found my high school review books. After a little skimming, I found a very similar model problem—within my 10th grade Amsco geometry review text. Then I remembered the difficulty I had with my first term of geometry in high school and all the extra help I needed to master and understand those theorems at the time. Now we expect a student to master concepts that used to be taught to 15-16 year old students thirty of so years ago. A 16 year old student is well into what Piaget calls the formal operational stage of development. Those are fancy words that mean that a student of that age can more easily understand very abstract concepts. Now we are supposed to expect a 13 year-old student to have the same capacity as a student that is very close to college age. Obviously, some 13 year-old students can understand such concepts, but most will have difficulty, again, because they may not be developmentally ready—especially if a disability is present. When I recently stated this at a meeting, I was told that I have low expectations for students. I replied that I do not have low expectations, but realistic expectations. And that these expectations are based on a good deal of scientific research.
83% of juniors with IEP's in RI are at risk of not graduating next year because of the NECAP math, 94% in the PPSD. Of course, they just have to improve a little, and nothing helps a special education student improve like pressure and fear.
Thursday, March 21, 2013
The Shape of Things to Come
Are there things about the Common Core that you don’t like?
No, not really, not conceptually. But I do worry somewhat about the assessments — I'm concerned that we may be headed for a train wreck there. The test items I've seen that have been released so far are extremely challenging. If I had to take a test that was entirely comprised of items like that, I'm not sure that I would pass it — and I've got a bunch of degrees. So I do worry that in some schools, we’ll have 80 percent or some large number of students failing. That's what I mean by train wreck. But who knows? We just don’t know enough about the assessments right now. But when I have shown some of those released items to groups of educators — to teachers and administrators — the room just goes very quiet. So I can imagine a hostile response on the part of some educators and communities. But I'd like to be wrong about that.
Teachers Migrate Upstream
John Thompson (making an important point while uncharacteristically losing control of his syntax, but hey, it's a blog):
It is unusual for high-performing teachers to leave their high-performing schools for low-performing or high-poverty schools. And many of them move to high-poverty, high-performing selective schools. But, Calder crunched this data for 13,456 secondary Reading teachers in two states. Only, 109 shifted to a higher-poverty school!
That's .8%.
Wednesday, March 20, 2013
We Have Definitely Established One Thing
11th grade students who suspect they won't get a "2" on the NECAP should make sure they get the lowest score possible on the test to make sure they have room to show improvement.
Luckily, we don't base any other important decisions on NECAP scores.
To Be Honest, This Is All Just Kabuki
The big question for Mercurio is about how to judge a student's improvement. If a student taking the test for the second time again fails to score a 2, that student could use the test for graduation if he showed growth.
"So the question is, how much is good enough when it comes to growth? What does that look like?" Mercurio said.
According to Gist, it would be “any growth that’s not by random chance - any growth at all that’s meaningful."
She said specific score targets are available now for every child but did not explain exactly how each target was calculated.
"The goal score will vary," she said via Twitter Monday night, "however, the calculation of growth is the same."
If the NECAP needs to be taken a third time, Gist said, the hardest questions would be culled from the test, with the idea of making it less intimidating. "But it doesn’t mean that it’s easier for them to get the score that they need to graduate."
When asked why that version of the test wasn't used for the second go-around, Gist said, "The range of why those students didn’t score a 2 varies really wildly - everything from they did their very best and they didn’t do very well, to they got really nervous and they didn’t do very well, to they just flat out didn’t try because they didn’t think it counted or it mattered. So there no need for us to make that determination until we’ve at least given it a second try."
Is This What Happens When You've Got a Multi-State Testing Consortium?
In the NCLB era, it has become a rule of thumb that Test Scores Go Up. That is, they are required to go up, and in aggregate, they do. This is partly because schools, teachers and kids adjust to the demands of a particular test over time, including but not limited to actual improvements in teaching and learning.
It is to at least to a small extent due to an increase in various kinds of cheating at the school level as pressures rise over time.
Finally, there is pressure to quietly make the tests easier in content or scoring. As Todd Farley recounts in Making the Grades, this may require no more than a visit to the scoring center from a mid-level state official and a quiet conversation behind closed doors about the "proper application of the approved rubric" to generate a different score distribution.
Or perhaps the cut scores are quietly moved in a technical meeting.
Or there's a presumption that making the tests a graduation requirement will lead to a large bump in scores, as was the case with the MCAS in Massachusetts.
From 2007 to 2012, the percentage of students in Rhode Island scoring Substantially Below Proficient has moved from 51% to 40%. The entire premise of using the NECAP for a graduation requirement is dependent on that number going down to no more than about 10% (at most!). That has to happen, or it will be politically untenable.
If you're used to looking at changes in state test scores over time in the abstract, it was reasonable to assume that this would "just work," because Test Scores Go Up but perhaps that doesn't factor in the quiet shenanigans by states and testing companies.
Because this is a multi-state testing consortium, RIDE can't wink-wink nudge-nudge the testing company and to get the scores up. Vermont and New Hampshire would have to agree as well, and since they aren't using the NECAP for graduation, they have no incentive to play along.
Again, this may be the shape of things to come in the Common Core era.
Be Careful What You Wish For in Assessment
The Common Core State Standards for mathematics, now being introduced in schools across the country, set new grade-by-grade expectations for deepening students' understanding of math concepts, with an emphasis on algebraic thinking.
But while many accomplished math teachers are enthusiastic about the standards' emphasis on mathematical reasoning and strategic expertise over rote computation, some say the transition to the new framework poses daunting challenges for students who are already behind in math.
"Every time I talk to other teachers, this issue comes up," said Silvestre Arcos, the founding math teacher at KIPP Washington Heights Middle School, a charter school in New York City. "The big question is, how do we build up these advanced skills with kids who come in behind?"
Students need "prerequisite knowledge" to meet the new grade-level expectations mapped out in the common standards, said José Vilson, who teaches 8th grade math at I.S. 52, a public middle school a in New York City's Inwood neighborhood. But by the time they reach him, students at his school—many of whom are English-language learners—often "have a lot of catching up to do," he said.
This is probably more or less what the situation already is with the NECAP math, but for some reason it doesn't really kick in until you hit the 11th grade version, or maybe the cut scores just go crazy at that point.
The problem is that if you've got a test that requires a deep, rich set of mathematical reasoning and problem solving skills, this might not cut it:
This year’s high school juniors already have access to math problems and tutors online. In addition, many districts are offering remedial help after school or during the summer.
What if you've created an assessment regime that is truly resistant to quick fixes and test prep? What do you do with kids who fall behind if it takes maximum effort to keep up at all? What if you run a query on your magic inBloom database that shows that anyone who has failed a year of math after seventh grade only has a 5% chance of ever getting over a "1" on the 11th grade NECAP math no matter what interventions you try subsequently?
Tuesday, March 19, 2013
Trying to Get the Lay of the New Data Interoperability Landscape
In the beginning (1997), there was SIF, which now touts itself as "the first, largest and most implemented open global standard for seamless, real time data transfer." I think "for schools" is implied. It was an oddball pain in the ass that required a lot of work for application developers to integrate and for most of the past 15 years you'd be paying a commercial vendor to set up a "zone integration server" for you. Google tells me there are finally a number of established open source options and that Pearson (surprise!) bought out the main SIF vendor. Importantly, SIF crowded everything else out through a period of revolutionary change in the web and web services, stunning successes for a few open standards (HTML, CSS...), and a number of partial ones (XML, RDF...).
I tuned this whole scene out for a while until it sorted itself out...
I think the turning point was the Common Educational Data Standards, sponsored by ed.gov in some way, which got rolling in 2009. It is a refinement of the existing core models for educational data and the core of all that follows. It is just "a set of commonly agreed upon names, definitions, option sets, and technical specifications for a given selection of data elements."
Since then, things have gotten cooking.
Ed-Fi is an expanded data model based on the CEDS and some dashboards and other tools and software I don't think anyone will really care about. It is sponsored by the Dell Foundation.
inBloom has a data model based on Ed-Fi, which probably expands it. It also importantly lays out a REST web services API for moving the data around, which is generally speaking the way I'd want to do it. They've also written some open source tools for getting data out of their giant repository, which is also supposed to be open sourced Real Soon Now. The creepy part is just that they really want ALL the data in THEIR inBloom repository. That's backed by Gates, Murdoch, etc.
OK, then we get to the startups. Clever and LearnSprout (probably there are more). They are kind of like a simpler version of SIF where they define a simple REST API, hook into your SIS and host the integration server. They get key student and enrollment data out of your SIS automatically, park it on their server, and other applications your school is using can easily pull it. It is the 80% of what schools want and need in this area, and I suspect they do a good job. It certainly makes sense for smaller schools -- charters -- at least. I would like to think larger districts can and should handle this themselves. If this is a hot startup it isn't saying much for the startup scene though, because I can't see it as more than a niche market and a transitory phase.
The best part is that we should end up with "rough consensus and running code" on some basic REST API's and underlying data model, which is a big deal.
So... what am I getting wrong in the above?
My Estimated NECAP Score
Apparently I came out somewhere in the "proficient" range on my mini-NECAP math, getting 67% right. That tells you something about the difficulty of the test questions when you do well to miss one in three.
I don't know in practice what percentage of questions a student would need to get right to get from a "1" to a "2," but I bet it is pretty low -- which seems easy I guess but it takes a lot of fortitude to stick with a test when you know you're getting more wrong than right. Especially if they don't order the questions from easiest to hardest. Our mock NECAP didn't, but I don't know about the real one.
In practice, graduation for a lot of kids may come down to not blowing your cool a few hours into this thing and making a few savvy guesses instead of putting your head down. That's easier, I'd note, if you weren't exposed to lead as a child.
How Would New Hampshire High School Students Do With Rhode Island's Graduation Requirements?
Some background numbers for New Hampshire:
- 2010-2011 graduation rate: 86% (3rd in US)
- 2011 Science and Engineering Readiness Index (SERI) ranking: 4th in US
- 4th grade scale score state rank: 2nd
- 4th grade % of students below basic: 8% (2nd)
- 8th grade scale score state rank: 6th
- 8th grade % of students below basic: 18% (4th)
2009 NAEP 11th Grade Mathematics Pilot (of 11 participating states)
- Scale score state rank: 2nd of 11
- % of students scoring below basic: 26% (3rd)
2012 NECAP Mathematics
- 4th grade % of students substantially below proficient: 8%
- 8th grade % of students substantially below proficient: 15%
- 11th grade % of students substantially below proficient: 36%
Percentage of current New Hampshire high school juniors who would be at risk of not graduating under Rhode Island's 2014 requirements: 36%
RI's Diploma Sequestration
The manufactured crisis continues:
The test left numerous participants shaking their heads over the difficulty of the questions, which ranged from geometry to probability, and more than a few suggested abandoning the test as a graduation requirement.
That provoked heated words from state Education Commissioner Deborah A. Gist, who called participants’ response to the test “an outrageous act of irresponsibility.”
“It’s deeply irresponsible on the part of the adults, especially those who are highly educated,” she said. “They’re sending a message that it can’t be done or that it doesn’t matter.”
Gist said once she saw the story, she realized how damaging it was.
“I spent a lot of time [this weekend] trying to convince students why it matters,” she said. “We need all of the adults rallying around these students rather than getting caught up in arguments that don’t have any substance.”
Eva-Marie Mancuso, the chairwoman of the new Rhode Island Board of Education, called the mock test a publicity stunt and said it was diverting attention from the real issue: preparing students to be successful in college and in the workplace.
“We don’t just give this test without any preparation,” Mancuso said. “If I was to take the bar exam tomorrow, I have no idea if I’d pass or not.”
An "outrageous act of irresponsibility" to take a short version of our high school graduation test? Or to suggest that perhaps there was a problem with using the NECAP for that purpose? Commissioner Gist is a true believer in the Green Lantern Theory of Education Reform -- if we just have sufficient will, we can do anything. If we all believe hard enough.
I also don't think she appreciates who was in that room on Saturday. It wasn't a bunch of lightweights and hippies; it was politicians and wonks. Not people who are going to be cowed or impressed by having their concerns dismissed as lacking substance.
This is the first time officials in Providence have said anything to Gist's RIDE other than "Thank you sir, may I have another?" and it is the first time middle class families are as directly affected as the urban poor. So... it should be interesting. Maybe it will just be settled by the legislature. You have multiple paths when the state is the size of a large county.
Chairwoman Mancuso seems to be falling into a common trap these days, having trouble holding the concept of an appropriate "minimum high school graduation requirement" in her head. I imagine I would have had trouble (re-)passing my senior calculus final by a few weeks into summer vacation, but what we're supposedly talking about is the minimum score to get a diploma at all. Give me the final for the lowest-level culminating math class to make a kid eligible for graduation, I bet I can pass that, and most college-educated professionals probably can too.
Monday, March 18, 2013
Hobby Update
Soupy coming along.

I actually cut into one last weekend because it had a bad spot:

It was still pretty raw in the middle. The hard part is trying to get them to dry uniformly throughout. I brought over a humidifier today to try to slow down the drying process and give it time to even out.
Also, more 19th century catching practice:
1880's Catching Practice 2 from Tom Hoffman on Vimeo.
You can tell Tony is a more experienced catcher, teacher and coach than me by the way he gives feedback after every pitch. I'm setting up higher with my feet closer together this week, and I think it is an improvement.
I watched a lot of wicket keeping tips on YouTube this week to get some ideas.
Sunday, March 17, 2013
My Notes from Taking a (Shortened) NECAP Math #takethetestpsu
I jotted some notes down in a corner of my scrap paper and smuggled it out of the testing site.
I had one moment of panic which I think reflects the kind of thing a lot of kids would go through on the test on a question that I thought was very emblematic of the exam. We had to analyze a sequence of fractions, which was tricky mostly because the second fraction had been reduced to lowest terms, which disguised the pattern. This was enough to convince my table neighbor, the Chair of the Providence City Council Education Committee, that there was an error in the test.
But also, the list was formatted oddly -- I'm not 100% sure that it was this way in the original NECAP -- with the commas separating the fractions floating just below the bar in the fraction, so it looked like the denominators might actually be 5', as in "five to the apostrophe," some notation I'd never heard of. For a few seconds I just froze and thought "5-apostrophe?!? This must be some new math we never covered in class!" Then I calmed down and decided it was just bad formatting. A lot of already rattled kids wouldn't make that recovery. If you actually talk to kids in city schools about these tests, they get hung up on that kind of thing all the time.
I eventually figured out that to find the answer you could go through the four choices of expressions for finding the 20th item in the sequence and see which one would correctly match the third or fourth fraction shown. I think I got it right, and it took some reasoning, but it whether or not that was math is an open question.
Another question I thought was typical showed two spinners that would give you random numbers from 1 to four. It wanted to know the probability that the sum of the two would be a prime number. I drew a complete blank, until I realized I could easily write out all 16 combinations and just circle the ones that resulted in a prime number. That more clearly took mathematical reasoning, problem solving and content knowledge.
I like the question, and I like the direction it should push math curriculum. But I'm also aware that if even if kids have been taught probability, if they haven't been taught it in a way that encourages flexible and resourceful problem solving -- rather than pulling numbers out of stereotypical word problems and following procedures -- they will be completely screwed.
On the whole, the NECAP math pushes for deep conceptual understanding, which is great, unless you don't have it and you need to pass the test to graduate. For a math test, I thought it required very little knowledge of terminology. In the sequence question I mentioned above, you needed to know the prime numbers between 2 and 8. There was one that required knowing the definition of sine and tangent (I guessed). Those were the exceptions though. It was about applying math in what seemed like odd abstract contexts. A lot of them, particularly the multiple choice but even some of the short answers, seemed solvable by what seemed like brute force approaches if you understood the concepts well enough to narrow down the possibilities quickly.
I have no idea if there are textbooks that are made up of questions like these. If there are, I didn't get the impression from the students running the event that PPSD uses them.
I didn't leave thinking that the NECAP was a bad test, but it is completely different from a test you would design from scratch as a graduation requirement.
Thanks to the Providence Student Union for putting this together.
Friday, March 15, 2013
Google Reader, Whatever
I can export all the data I really need out of Google Reader and imported into whatever RSS reading I decide to start using before July, so what's the big deal?
LearnBoost and Having Nice Things
Audrey Watters:
LearnBoost launched at the beginning of this recent resurgence in ed-tech entrepreneurialism, and in many ways, I thought it encapsulated much of the promise that new ed-tech startups are supposed to hold: great technology, great product, great team, grassroots adoption, freemium pricing, and so on.
To me, (co-founder and CEO Rafael) Corrales’ departure now serves to highlight some of the serious tensions, if not grave problems, that this new “ed-tech ecosystem” is facing. Indeed, what sort of “ed-tech ecosystem” are we really building here? Will it thrive? Which startups will survive? Whose values does this “ecosystem” reflect?
I admit I haven't paid any attention to LearnBoost, despite its being a competitor to SchoolTool (which I manage). Just looking at their website it isn't apparent how this is a business at all. I guess it is a "freemium" model, but usually there is something explaining what you might pay for. The product seems to be primarily aimed at individual teachers, not schools or districts.
Googling... ok, here's an explanation from Corrales:
Our intention is to keep our software free for teachers, parents, students, and even admins while having anyone who wants customization or extra support and services to pay a fraction of what the current systems charge. That's pretty powerful - we're going to save schools in the U.S. hundreds of millions of dollars a year, and globally we're aiming to save schools even more money.
Unlike our competitors in this space, we're well funded by the investors that backed Skype, LinkedIn, Twitter, and more. We're going to be around for a really long time.
OK, but that's a super low margin business. And that's based on my analysis as someone who is going to be pursuing the same strategy. I'm not sure if it will be enough to maintain the not-so-lavish lifestyle of me and one partner, let alone pay off for an investor.
And while common academic and data interoperability standards should be a boon to adoption in this business, won't standardization also, by definition, dramatically reduce the need for customization and support services, at least in the US?
It is hard for me not to conclude that the purpose of this company was always to develop some great technology and sell out to a big player. It doesn't make much sense otherwise.
Having said all that, I am a bit jealous of their technology. Timing is huge in a rapidly changing technological environment, and we ended up laying the foundations of SchoolTool right before everything changed in web development, and that's a cross we simply have to bear (or give up entirely).
Regarding open source, Watters praises LearnBoost and co-founder Guillermo Rauch for open sourcing lots of new infrastructure developed for their platform. And yes, that is a good thing. But also it is funny because while SchoolTool is 100% open source, one of the few hard rules Mark Shuttleworth gave for the use of his funding was to absolutely not hire web platform hackers and let them spend time writing generic infrastructure instead of application specific features. In general, it'll always be more in a geek's comfort zone to write, say, "the implementation of transport-based cross-browser/cross-device bi-directional communication layer for Socket.IO" than, say, a robust versioning system for academic standards or some other tricky business logic. It may work out fine for them, but it is a risky and expensive approach.
Also, open sourcing this stuff is admirable and helps the node.js community, but doesn't really do anything for the education community.
Regarding usability, if you're really writing enterprise software, the tradeoffs aren't so clear sometimes. For example, importing standards into LearnBoost takes one worksheet in a spreadsheet, whereas for SchoolTool it takes five. It probably takes two or three times as long in SchoolTool to get them set up. On the other hand, once you have that extra metadata, in there, you can automatically assign the correct standards to all the relevant courses in your school with one click -- saving you a lot more time in the end, but that's not obvious in a casual preview of the product. Our method is more abstract and probably does require more manual reading and maybe training, but it would save a ton of time over the years.
Regarding exporting your data, the big problem has been the lack of a standard format for doing so, particularly one that can handle complex school or district-wide data. Even if you want to dump the whole database in some easily reusable form, there's just not been clear method. Hopefully that's rapidly changing finally.
I don't want to end this on an "abandon all hope" note, because, oddly, inBloom may finally be breaking the ice to make the real solution politically viable. That is, big foundations just saying "Screw it, we'll just pay vendors with experience more or less successfully writing software used in schools to develop the open source infrastructure we want." Isn't that what Gates and Amplify did with inBloom? If that works, why not apply the same principle elsewhere?
Thursday, March 14, 2013
Tom Sgouros Looks at NECAP Math
After consulting these appendices, you will see that — at the time they were chosen — the cut scores for the 11th grade math test put 46.5% of all test takers in the “substantially below proficient” category (see page 19 of Appendix F 2007-08). This is almost four times as many students as were in that category for the 11th grade reading test and more than twice as many for any other NECAP test in the other grades.
Tom also explains at length the difference between "a test like NECAP, designed to rank schools and students, and a test designed to evaluate student proficiency," but to me the bottom line is the cut scores.
Russo Asks a Good Question
Russo:
If you're going to do edtech, for example, why not do universal access?
The reason is that universal access challenges actually powerful interests (compared to, say, poor families and urban schoolteachers) and would make conservatives angry:
- You'd have to flood the country with low end tablets and netbooks purchased in bulk at a discount, wrecking part of the market (which would make a lot of ed-tech advocates sad because they wouldn't be getting the latest and shiniest).
- You'd have to give away a lot of high speed internet, screwing up not only the internet services market but also TV and phone service, since you more or less get those with the internet now.
- You'd drive conservatives insane by giving, for example, every single mother with three kids living on public assistance three free computers and high speed internet.
Every ed-tech advocate should have (like me) a 12 year old neighbor who for a few weeks at a time will come over once a day to make phone calls for herself and her family because they've not been able to keep up with their phone bills. It is a good reality check.
Also True About Education
Michael Ruhlman:
The data that matters to me is the data I receive after I’ve finished eating something. Do I feel good after eating a roast chicken with gravy and mashed potatoes and a pile of shaved sautéed Brussels sprouts? Yes. How about after I eat a bag of Cheetos? Not so good. What does that mean? Think about it. Think. Do you feel good after you exercise? Yes, because it’s good for you. Or you can hunt for data on the Internets if you want The Truth. Go ahead, read up on it. Or watch all the “a new study finds” stories on the ABC Nightly News.
Wednesday, March 13, 2013
Sabrina Joy Stevens Writes it So I Don't Have To
Sabrina Joy Stevens:
Remember: schools are part of a community ecosystem. We have the right and responsibility to ensure public officials don’t replace the symbiotic relationships that school employees have within the community, with potentially parasitic relationships with faraway companies who would take from our public coffers without necessarily putting enough back in.
A true commitment to personalized learning requires a renewed appreciation of the persons who make it possible. Tech is great, but let’s get real: no app ever painted a classroom, or hand-sewed pillows so its students could have cozy places to learn to love reading. No smart board ever improvised a harmony with its student’s rising voice, teaching a new skill and inspiring a new song in the process. And no computer ever offered a warm smile or embrace to comfort a traumatized child, or food to a child without enough to eat. Teachers and other school employees do all of these things and more. We should be finding ways to keep them where they can protect, nurture and teach students, not finding ways to get away with fewer and fewer of them.
We Just Beat Out Worcester's Plan to Cut Obesity Through Telescreen Calisthenics
Jennifer Steinhauer:
Providence took the grand prize for its plans to improve early childhood literacy. The children who participate in the program would wear a small device called a digital language processor that would record their daily interactions with adults. Those would then be converted into audio files containing the day’s adult word count and the number of conversational turns. That data would be used to help parents in monthly coaching sessions improve the quality of their conversations to improve their children’s vocabulary.
It does sound like a useful project, but lately all the good news seems to come with a side dish of creepy.
If you're curious, here's a 2008 article on the technology in the NY Times.
Tuesday, March 12, 2013
billg Reads an Informational Text
I should first note that while I read the Why Nations Fail blog, I've not read the book.
With that disclaimer, Bill Gates's negative review of Why Nations Fail is... interesting. First off, it is pretty clearly just billg knocking out a long post, perhaps completely unedited. Real blogging! It certainly has some quirks, like referring to Daron Acemoglu and James Robinson only as "the authors," and a general certainty that Acemoglu and Robinson are wrong because Gates's interpretation of history is correct:
The authors demonstrate an oddly simplistic world view when they attribute the decline of Venice to a reduction in the inclusiveness of its institutions. The fact is, Venice declined because competition came along. The change in the inclusiveness of its institutions was more a response to that than the source of the problem. Even if Venice had managed to preserve the inclusiveness of their institutions, it would not have made up for their loss of the spice trade.
Acemoglu and Robinson respond:
This is just bad history. Venice didn't decline because of the loss of the spice trade. If that were the case, the decline should have started at the very end of the 15th century. But the decline was already well underway by the middle of the 14th century. More generally, research by Diego Puga and Daniel Trefler shows that Venice's fortunes had nothing to do with competition or the spice trade.
Abstract: International trade can have profound effects on domestic institutions. We examine this proposition in the context of medieval Venice circa 800-1350. We show that (initially exogenous) increases in long-distance trade enriched a large group of merchants and these merchants used their new-found muscle to push for constraints on the executive i.e., for the end of a de facto hereditary Doge in 1032 and for the establishment of a parliament or Great Council in 1172. The merchants also pushed for remarkably modern innovations in contracting institu- tions (such as the colleganza) that facilitated large-scale mobilization of capital for risky long-distance trade. Over time, a group of extraordi- narily rich merchants emerged and in the almost four decades following 1297 they used their resources to block political and economic competi- tion. In particular, they made parliamentary participation hereditary and erected barriers to participation in the most lucrative aspects of long-distance trade. We document this ‘oligarchization’ using a unique database on the names of 8,103 parliamentarians and their families’ use of the colleganza. In short, long-distance trade first encouraged and then discouraged institutional dynamism and these changes operated via the impacts of trade on the distribution of wealth and power.
Of course, I find this amusing in light of the Common Core ELA standards. I'll leave scoring Gates's post against the standards as an exercise for the reader, but I would note that Gates does a particularly poor job with standard 1 ("...cite specific textual evidence...") and this points out the difficulty of scoring standard 8 ("...evaluate the argument and specific claims...") since, for example, there is no answer key in the Teacher's Edition with the real reasons Venice fell.
Also, the CC ELA pointedly does not allow the reader to cite the author's biases, for example, if he is a reviewing a book that directly challenges his role as an insanely wealthy monopolist philanthropist.
In Case You Wonder What's Going in inBloom
- Alternative/Supplemental Services Domain
- Assessment Domain
- Career and Technical Education Domain
- Discipline Domain
- Education Organization Domain
- Enrollment Domain
- Graduation Domain
- School Calendar Domain
- Special Education Domain
- Staff Domain
- Student Academic Record Domain
- Student Attendance Domain
- Student Cohort Domain
- Student Identification and Demographics Domain
- Teaching and Learning Domain
- AcademicHonor
- AcademicSubjectsType
- AcademicWeek
- AccountabilityRating
- AdditionalCredits
- Address
- Assessment
- AssessmentIdentificationCode
- AssessmentItem
- AssessmentPerformanceLevel
- AssessmentPeriodDescriptor
- Attendance
- AttendanceEvent
- BehaviorDescriptor
- BehaviorDescriptorType
- BirthData
- CalendarDate
- ClassRanking
- Cohort
- CohortYear
- CompetencyLevelDescriptor
- CompetencyLevelDescriptorType
- Course
- CourseCode
- CourseOffering
- CourseTranscript
- Credential
- CredentialFieldDescriptor
- Credits
- CreditsByCourse
- CreditsBySubject
- CTEProgram
- Diploma
- Disability
- DisciplineAction
- DisciplineDescriptor
- DisciplineDescriptorType
- DisciplineIncident
- EducationalOrgIdentityType
- EducationOrganization
- EducationOrgIdentificationCode
- ElectronicMail
- EmploymentPeriod
- FeederSchoolType
- Grade
- GradebookEntry
- GradingPeriod
- GradingPeriodIdentityType
- GraduationPlan
- Home
- InstitutionTelephone
- LearningObjective
- LearningObjectiveIdentityType
- LearningStandard
- LearningStandardId
- LearningStandardIdentityType
- LearningStyles
- Links
- LocalEducationAgency
- MiscellaneousEvent
- Name
- ObjectiveAssessment
- OtherName
- Parent
- PerformanceLevelDescriptor
- PostSecondaryEvent
- Program
- ProgramParticipation
- Recognition
- ReportCard
- RestraintEvent
- RestraintEventReasonsType
- School
- SchoolYearAttendanceType
- ScoreResult
- SecondaryBehavior
- Section
- ServiceDescriptor
- ServiceDescriptorType
- Session
- Staff
- StaffCohortAssociation
- StaffEducationOrganizationAssociation
- StaffIdentificationCode
- StaffProgramAssociation
- StateEducationAgency
- Student
- StudentAcademicRecord
- StudentAssessment
- StudentAssessmentItem
- StudentCharacteristic
- StudentCohortAssociation
- StudentCompetency
- StudentCompetencyObjective
- StudentCompetencyObjectiveReference
- StudentCTEProgramAssociation
- StudentDisciplineIncidentAssociation
- StudentGradebookEntry
- StudentIdentificationCode
- StudentIndicator
- StudentObjectiveAssessment
- StudentParentAssociation
- StudentProgramAssociation
- StudentSchoolAssociation
- StudentSectionAssociation
- StudentSpecialEdProgramAssociation
- Teacher
- TeacherSchoolAssociation
- TeacherSectionAssociation
- Telephone
- WeaponsType
- AcademicHonorsType
- AcademicSubjectType
- AdditionalCreditType
- AddressType
- AdministrationEnvironmentType
- AdministrativeFundingControlType
- AssessmentCategoryType
- AssessmentIdentificationSystemType
- AssessmentItemResultType
- AssessmentReportingMethodType
- AttendanceEventCategoryType
- AttendanceEventType
- BehaviorCategoryType
- CalendarEventType
- CareerPathwayType
- CharterStatusType
- ClassroomPositionType
- CohortScopeType
- CohortType
- CohortYearType
- ContentStandardType
- CountryCodeType
- CourseAttemptResultType
- CourseCodeSystemType
- CourseDefinedByType
- CourseGPAApplicabilityType
- CourseLevelCharacteristicItemType
- CourseLevelType
- CourseRepeatCodeType
- CredentialType
- CreditType
- DiplomaLevelType
- DiplomaType
- DisabilityType
- DisciplineActionLengthDifferenceReasonType
- EducationalEnvironmentType
- EducationalPlanItemType
- EducationOrganizationCategoryType
- EducationOrgIdentificationSystemType
- ElectronicMailAddressType
- EmploymentStatusType
- EntryType
- EnvironmentType
- ExitWithdrawType
- GenerationCodeSuffixType
- GPAWeightedType
- GradeLevelType
- GradeType
- GradingPeriodType
- GraduationPlanType
- IdeaEligibilityType
- IncidentLocationType
- InstitutionTelephoneNumberType
- ItemCategoryType
- LanguageItemType
- LEACategoryType
- LeaveEventCategoryType
- LevelOfEducationType
- LevelType
- LimitedEnglishProficiencyType
- LinguisticAccommodationItemType
- MagnetSpecialProgramEmphasisSchoolType
- MediumOfInstructionType
- MeetingDayItemType
- MethodCreditEarnedType
- OldEthnicityType
- OperationalStatusType
- OtherNameType
- PerformanceBaseType
- PersonalInformationVerificationType
- PersonalTitlePrefixType
- PopulationServedType
- PostingResultType
- PostSecondaryEventCategoryType
- ProgramAssignmentType
- ProgramSponsorType
- ProgramType
- RaceItemType
- ReasonExitedType
- ReasonNotTestedType
- RecognitionType
- RelationType
- RepeatIdentifierType
- ReporterDescriptionType
- ResponseIndicatorType
- RestraintEventReasonItemType
- RetestIndicatorType
- SchoolCategoryItemType
- SchoolFoodServicesEligibilityType
- SchoolType
- SchoolYearType
- Section504DisabilityItemType
- SeparationReasonType
- SeparationType
- SexType
- SpecialAccommodationItemType
- StaffClassificationType
- StaffIdentificationSystemType
- StateAbbreviationType
- StudentCharacteristicType
- StudentIdentificationSystemType
- StudentParticipationCodeType
- TeachingCredentialBasisType
- TeachingCredentialType
- TelephoneNumberType
- TermType
- TitleIPartAParticipantType
- TitleIPartASchoolDesignationType
- WeaponItemType